Fixed fractional money management affects how your trades turn out overall. Keep in mind that trading is the sum of several hundred trades. After a few hundred trades or more, the power of money management starts to show.
As I discussed last week in modeling money management, trading completely at random with a 50% winning chance and a R multiple of 1 does not produce an advantage. The average win divided by the average loss is known as a R multiple. Such a system has neither benefits nor drawbacks. The average result ought to be quite close to the initial balance.
The bell curve is compressed in some areas and stretched in others when fixed fractional money management is used. It’s crucial to keep in mind what fixed fractional money management entails before we proceed. It has a fancy name for a straightforward idea. It represents the notion of risking a predetermined portion of the equity in the current account rather than the initial equity.
Most traders prioritize risking a predetermined sum of money, like $1,000, on a particular deal. After each trade, this procedure changes that dollar amount.
Take into account a scenario where 1% of the account’s initial $100,000 balance is at danger. On the initial trade, the risk for both strategies is $1,000. The risk level for the subsequent trade, however, will be different. If the prior deal was successful, the account equity would rise to $101,000. The risk on the following trade is $1,010 or one percent of 101 grand. ten dollars and change, whoa.
It could appear unimportant. Over the long term, it very definitely is not.
Examples
Think about a trader that participates in the coin toss game and uses a method that has the following qualities:
- He starts with a $100, 000 account balance
- His R multiple is 1.0
- He wins 50% of the time with no trading costs
- He risks 1%
A loss of $46,000 is the worst possible result when playing the coin toss with a fixed dollar stake of $1,000. When fixed fractional money management is used during a tough drawdown, the loss is reduced to $37,500. The worst decline is between -46% and -37.5%. By using this strategy, the worst-case situation is dragged down toward the average. The strategy lessens the trader’s losses when an unfortunate, disastrous decline begins.
A $58,000 (58%) return is the best case scenario for fixed dollar risk. The best case scenario is drastically shifted to the right by include money management in the system. The return increases to $76,000 (76%). Without making any changes to the trading mechanism, the good times get a lot better. The strategy deviates from the norm in terms of positive returns. The trader leaves with a larger profit in his wallet.
The default assumption is that fixed fractional money management is the best course of action. I concur. It enhances a completely random strategy’s risk-reward profile. It should aid in regulating variables that most traders deem crucial, such as drawdowns and return maximization, when added to a genuine trading system.
However, a significant side effect of fixed fractional money management is a little increase in the likelihood of earning a return that is below average. 47% of the time, the coin toss game had a poor return. The probability of a return below average increased to 53% when fixed fractional money management was used. The impact is not very great. It’s more likely to lose. However, when it does, the “loss” is so insignificant that it can be said to be at break-even point.
Sometimes, seemingly random patterns, such as loss-win-loss-win, are observed in random numbers. When this happens, the size of trades on losers is greater than trades on winners. Even if the winning percentage is exactly 50%, the losers will still significantly outweigh the winners. The minor increase in risk of not making as much money as anticipated is caused by the micro effect of slightly higher losses than gains.
Graphing all outcomes
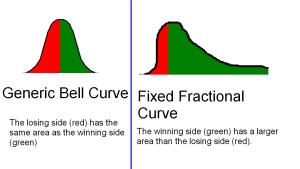
Losing results are represented by red areas, and winning outcomes are represented by green areas. The goal of effective money management is to increase the ratio of green to red areas. A bell curve, which may be seen on the left, results from random trades with no expectation of reward.
The highest density of returns is slightly shifted to the left by fixed fractional. This has the minor drawback of slightly raising the probability of insignificant loss. The extreme left side, which represents the worst-case loser, is dragged noticeably closer to the average. The far right (the best-case winner) deviates greatly from the norm. The green region has now surpassed the red area in size. There is a slim chance that the random system will provide a profit!







